Trong thế giới dự đoán số học, phương pháp soi cầu pascal đã trở thành một công cụ được nhiều người quan tâm và áp dụng. Dựa trên tam giác Pascal – một khái niệm toán học cổ điển được phát triển bởi nhà toán học Blaise Pascal, phương pháp này không chỉ đơn thuần là việc dự đoán ngẫu nhiên mà còn dựa trên những quy luật toán học cụ thể. Bài viết này gi8 sẽ giúp bạn hiểu rõ về phương pháp soi cầu pascal, cách thức hoạt động và những điều cần lưu ý khi áp dụng.
Tổng quan về phương pháp soi cầu pascal
Phương pháp soi cầu pascal không phải là một khái niệm mới mẻ, mà có nguồn gốc từ tam giác Pascal – một cấu trúc toán học được hình thành từ thế kỷ 17. Trong việc áp dụng vào dự đoán số học, phương pháp này tận dụng các quy luật và mẫu hình xuất hiện trong tam giác Pascal để tạo ra những dự đoán có tính hệ thống.
Nguồn gốc và lịch sử của phương pháp soi cầu pascal
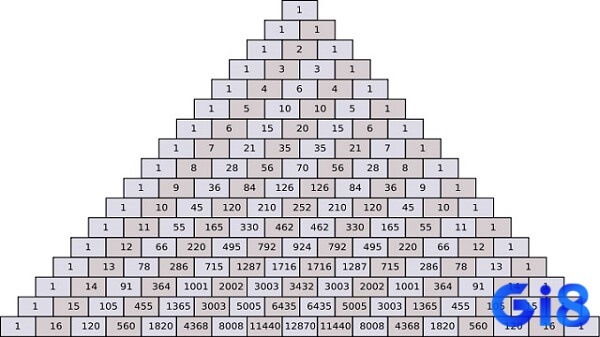
Tam giác Pascal được đặt tên theo nhà toán học và triết gia người Pháp Blaise Pascal (1623-1662), mặc dù cấu trúc này đã được biết đến từ nhiều thế kỷ trước đó ở các nền văn minh khác. Trong tam giác này, mỗi số được tạo thành từ tổng của hai số nằm ngay phía trên nó, tạo ra một cấu trúc đối xứng và chứa đựng nhiều quy luật toán học thú vị.

Khi áp dụng vào lĩnh vực dự đoán số học, phương pháp soi cầu pascal tận dụng các tính chất đặc biệt của tam giác Pascal như tính đối xứng, quy luật tổng và các mẫu hình lặp lại. Điều này tạo ra một hệ thống dự đoán không hoàn toàn dựa vào may rủi mà có một nền tảng logic toán học nhất định.
Đặc điểm cơ bản của phương pháp pascal
Phương pháp soi cầu pascal có những đặc điểm riêng biệt so với các phương pháp dự đoán khác. Đầu tiên, nó dựa trên cấu trúc tam giác Pascal với quy luật rõ ràng về cách hình thành các số. Thứ hai, phương pháp này tận dụng các tính chất toán học như tổng các số trong mỗi hàng, mẫu hình xuất hiện và quy luật lặp lại.
Một điểm đáng chú ý khác của phương pháp soi cầu pascal là tính hệ thống và logic trong cách tiếp cận. Thay vì dự đoán ngẫu nhiên, người sử dụng phương pháp này sẽ theo dõi các mẫu hình, phân tích xu hướng và đưa ra dự đoán dựa trên những quy luật đã được quan sát.
Nguyên lý hoạt động của phương pháp soi cầu pascal
Để hiểu rõ cách thức hoạt động của phương pháp pascal, chúng ta cần nắm vững các nguyên lý cơ bản và cách áp dụng chúng vào thực tế. Phương pháp này không chỉ dừng lại ở việc hiểu tam giác Pascal mà còn cần biết cách chuyển đổi các quy luật toán học thành công cụ dự đoán hiệu quả.
Cấu trúc tam giác phương pháp pascal
Cấu trúc này tạo ra một mẫu hình đối xứng với nhiều tính chất toán học đặc biệt. Trong phương pháp soi cầu pascal, các số trong tam giác này được chuyển đổi và phân tích để tìm ra các mẫu hình có thể áp dụng cho dự đoán.

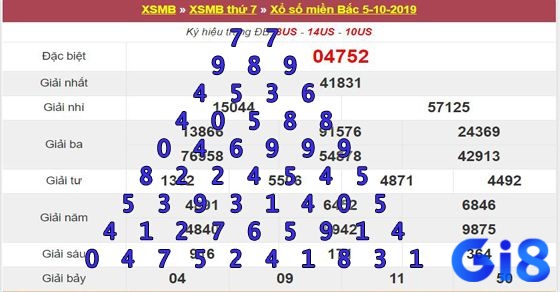
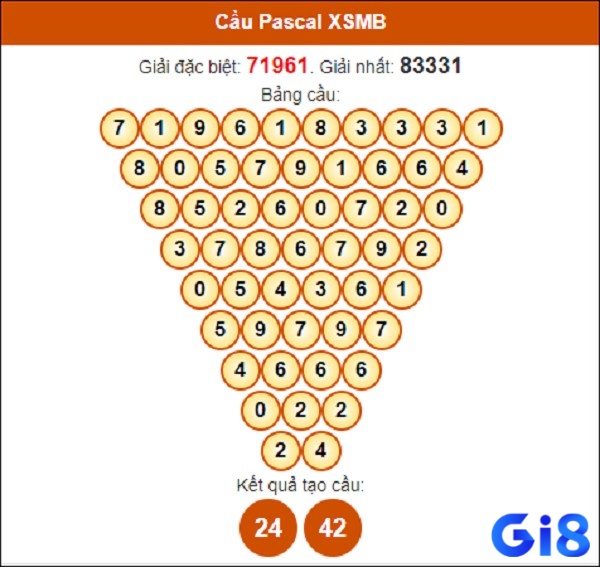
Việc áp dụng cấu trúc tam giác Pascal vào dự đoán số học thường bao gồm việc lấy các chữ số cuối của mỗi số trong tam giác, tạo ra một chuỗi số mới. Chuỗi số này sau đó được phân tích để tìm ra các mẫu hình lặp lại, xu hướng và quy luật có thể sử dụng cho dự đoán.
Quy luật và mẫu hình trong phương pháp soi cầu pascal
Phương pháp soi cầu pascal dựa trên việc nhận diện và khai thác các quy luật xuất hiện trong tam giác Pascal. Một số quy luật cơ bản bao gồm tính đối xứng của tam giác, tổng các số trong mỗi hàng tạo thành lũy thừa của 2, và các mẫu hình lặp lại trong chuỗi chữ số cuối.
Mẫu hình chu kỳ là một trong những yếu tố quan trọng nhất trong phương pháp pascal. Khi phân tích các chữ số cuối của tam giác Pascal, người ta nhận thấy sự xuất hiện của các chu kỳ lặp lại với độ dài khác nhau. Việc nhận diện được những chu kỳ này giúp dự đoán các số có thể xuất hiện trong tương lai.
Hướng dẫn chi tiết cách áp dụng phương pháp soi cầu pascal
Để áp dụng hiệu quả phương pháp soi cầu pascal, bạn cần nắm vững các bước cơ bản và những kỹ thuật nâng cao. Cần sự kiên nhẫn, tỉ mỉ và khả năng phân tích logic để có thể đưa ra những dự đoán chính xác.
Bước chuẩn bị khi sử dụng phương pháp pascal
Trước khi bắt đầu áp dụng phương pháp pascal, bạn cần chuẩn bị đầy đủ các công cụ và kiến thức cần thiết. Đầu tiên, hãy tìm hiểu kỹ về cấu trúc tam giác Pascal và các tính chất toán học của nó. Việc hiểu rõ nguyên lý cơ bản sẽ giúp bạn áp dụng phương pháp một cách hiệu quả hơn.
Bạn cũng cần chuẩn bị các công cụ hỗ trợ như giấy bút để ghi chép, máy tính để thực hiện các phép tính phức tạp, và một hệ thống ghi chú để theo dõi các mẫu hình và kết quả. Việc tạo ra một không gian làm việc tĩnh lặng và tập trung cũng rất quan trọng để đảm bảo tính chính xác trong quá trình phân tích.
Các bước thực hiện phương pháp pascal
Bước đầu tiên trong việc áp dụng phương pháp pascal là xây dựng tam giác Pascal với số hàng phù hợp. Thông thường, bạn nên tạo ra ít nhất 10-15 hàng để có đủ dữ liệu phân tích. Sau khi có tam giác Pascal hoàn chỉnh, bạn sẽ trích xuất các chữ số cuối của mỗi số trong tam giác để tạo ra chuỗi dữ liệu mới.
Tiếp theo, bạn cần phân tích chuỗi dữ liệu này để tìm ra các mẫu hình lặp lại. Quá trình này bao gồm việc nhóm các số theo chu kỳ, tính toán tần suất xuất hiện của từng số, và xác định các xu hướng có thể dự đoán được. Việc ghi chép tỉ mỉ mọi mẫu hình quan sát được sẽ giúp bạn xây dựng một hệ thống dự đoán hoàn chỉnh.
Kỹ thuật nâng cao trong phương pháp pascal
Một trong những kỹ thuật này là kết hợp phương pháp soi cầu pascal với các phương pháp phân tích khác như phân tích thống kê hoặc phân tích xu hướng.
Kỹ thuật khác là sử dụng các biến thể của tam giác Pascal, chẳng hạn như tam giác Pascal modulo (chia lấy dư) với các số khác nhau. Điều này tạo ra những mẫu hình mới và có thể cung cấp góc nhìn khác biệt về dữ liệu. Việc thử nghiệm với các modulo khác nhau như 2, 3, 5, 7 có thể mang lại những kết quả thú vị.
So sánh phương pháp soi cầu pascal với các phương pháp khác
Để đánh giá đúng giá trị của phương pháp pascal, chúng ta cần so sánh nó với các phương pháp dự đoán khác đang được sử dụng phổ biến. Việc hiểu rõ những điểm khác biệt sẽ giúp bạn lựa chọn phương pháp phù hợp nhất.
| Tiêu chí | Phương pháp Pascal | Phương pháp thống kê | Phương pháp truyền thống |
|---|---|---|---|
| Nền tảng lý thuyết | Toán học cổ điển | Thống kê hiện đại | Kinh nghiệm thực tế |
| Độ phức tạp | Trung bình | Cao | Thấp |
| Tính hệ thống | Cao | Rất cao | Thấp |
| Dễ học | Trung bình | Khó | Dễ |
Những lưu ý quan trọng khi áp dụng phương pháp soi cầu pascal
Để đạt được kết quả tốt nhất khi sử dụng phương pháp pascal, bạn cần lưu ý một số điểm quan trọng. Những lưu ý này không chỉ giúp tăng độ chính xác mà còn giúp bạn tránh được những sai lầm phổ biến trong quá trình áp dụng.
Yếu tố tâm lý trong phương pháp pascal
Sự kiên nhẫn và tỉ mỉ là những phẩm chất cần thiết vì quá trình phân tích và dự đoán thường mất nhiều thời gian. Người sử dụng cần duy trì tâm lý ổn định và không bị ảnh hưởng bởi cảm xúc khi đưa ra quyết định.
Việc quản lý kỳ vọng cũng rất quan trọng khi sử dụng phương pháp pascal. Mặc dù phương pháp này có nền tảng toán học vững chắc, nhưng nó vẫn không thể đảm bảo kết quả 100% chính xác. Người sử dụng cần hiểu rõ điều này và có thái độ thực tế về khả năng của phương pháp.
Thời điểm và tần suất áp dụng phương pháp soi cầu pascal
Việc lựa chọn thời điểm phù hợp để áp dụng phương pháp soi cầu pascal có thể ảnh hưởng đến kết quả. Nên dành thời gian tập trung, tránh mệt mỏi hoặc phân tâm. Một môi trường yên tĩnh và thoải mái sẽ giúp bạn phân tích chính xác hơn.
Tần suất sử dụng phương pháp pascal cũng cần được cân nhắc cẩn thận. Việc áp dụng quá thường xuyên có thể dẫn đến sự mệt mỏi và giảm độ chính xác. Ngược lại, sử dụng quá ít có thể làm bạn mất đi sự nhạy bén trong việc nhận diện mẫu hình.
Cách ghi chép và theo dõi kết quả
Bạn nên tạo ra một hệ thống ghi chú chi tiết để theo dõi các mẫu hình đã phát hiện, kết quả dự đoán và độ chính xác của từng lần áp dụng. Điều này giúp bạn đánh giá và cải thiện kỹ thuật của mình theo thời gian.

Việc phân tích định kỳ các kết quả đã ghi chép sẽ giúp bạn nhận ra những điểm mạnh và yếu trong cách áp dụng phương pháp soi cầu pascal. Từ đó, bạn có thể điều chỉnh chiến lược và phương pháp tiếp cận để đạt được kết quả tốt hơn.
Kết luận
Phương pháp soi cầu pascal là một công cụ dự đoán thú vị với nền tảng toán học vững chắc, mang lại cách tiếp cận có hệ thống và logic trong việc phân tích số học. Thông qua việc tận dụng các tính chất đặc biệt của tam giác Pascal, phương pháp này cung cấp một góc nhìn khác biệt so với các phương pháp dự đoán truyền thống.
Để áp dụng thành công phương pháp soi cầu pascal, bạn cần nắm vững các nguyên lý cơ bản, thực hành thường xuyên và phát triển kỹ năng phân tích mẫu hình. Sự kiên nhẫn, tỉ mỉ và thái độ thực tế về khả năng của phương pháp cũng là những yếu tố quan trọng không thể bỏ qua.
Hãy bắt đầu học và thực hành phương pháp soi cầu pascal một cách từ từ, tập trung vào việc hiểu rõ các nguyên lý cơ bản trước khi tiến đến những kỹ thuật nâng cao. Với sự nỗ lực và kiên trì, bạn có thể phát triển được kỹ năng sử dụng phương pháp này một cách hiệu quả và đạt được những kết quả tích cực.
